It's been 4 f**king years since the Fiers paper dropped and Bhasin is still taking a firm stance on backing TruT™algorithm (cFTZ).
As you should very well know it has been validated in Phase 1.
*In phase I studies, we demonstrated that the TruTTM algorithm provides accurate free T values that match those obtained using the equilibrium dialysis in healthy and hypogonadal men. We have also shown that the binding parameters that have formed the basis of previous equations (e.g., Vermeulen) are incorrect, and that free T values derived using these equations deviate substantially from free T measured by equilibrium dialysis. The phase I studies have led to the adoption of the TruTTM algorithm at several institutions.
A multi-step, dynamic allosteric model of testosterone’s binding to sex hormone binding globulin (2014) [PDF]
Mikhail N. Zakharov, Shalender Bhasin, Thomas G. Travison, Ran Xue, Jagadish Ulloor, Ramachandran S. Vasan, Emma Carter, Frederick Wu, Ravi Jasuja
Corrigendum to “A multi-step, allosteric model of testosterone's binding to sex hormone binding globulin” [Mol. Cell. Endocrinol. 399 (2015) 190e200] [PDF]
*Based on our analyses of the experimental data of testosterone’s binding to SHBG, we constructed a novel multistep binding model with complex intra-dimer allostery for the calculation of FT, which provided the best fit to the totality of experimental data. This new model was then utilized to determine FT concentrations in samples derived from randomized testosterone trials in men and women and to compare the results with those obtained using equilibrium dialysis. Finally, we used the algorithm to examine the distribution of FT levels in community-dwelling men in the Framingham Heart Study (FHS) and related the deviations from the mean to the risk of sexual symptoms and elevated LH levels in an independent sample of men in the European Male Aging Study (EMAS).
3. Results
3.1. Prevailing model of SHBG: T interaction is erroneous and results in significant deviation in calculated free T. We conducted a systematic evaluation of calculated free T values using the extant SHBG: T interaction model (cFTv) in two, placebo-controlled, randomized clinical trials in men and women receiving testosterone supplementation (TED and TEAM). Preliminary studies revealed that cFT values obtained using Vermeulen’s equation in samples derived from the TED Trials were systematically lower than those measured by equilibrium dialysis. To determine the molecular basis of this discrepancy, we used three experimental approaches to characterize testosterone’s binding to SHBG: binding isotherms by varying testosterone concentrations at a fixed SHBG concentration, ligand depletion curves by varying SHBG concentrations at a fixed testosterone concentration, and isothermal titration calorimetry (ITC).
5. Conclusions
In summary, experimental data generated using several independent methods provide evidence of an allosteric mechanism of testosterone binding to SHBG dimer. FT concentrations derived using the new dynamic model incorporating multistep interaction with allostery do not differ significantly from those measured using equilibrium dialysis in men and significantly reduce the systematic deviation in cFT values in women. The application of the new model to clinical trials data has revealed new insights into the percent of circulating testosterone that is free and the relation between percent FT and total testosterone and SHBG. The use of additional experimental models, including dimerization-deficient SHBG mutants, would allow further insights into molecular mechanisms of testosterone’s interaction with SHBG. The extension of the new dynamic model incorporating allostery should also be further explored in clinical populations as its availability on desktops and mobile devices can provide a convenient and accurate approach for determining FT at the point-of-care, and facilitating the diagnosis and treatment of men and women with androgen disorders.
A Reappraisal of Testosterone’s Binding in Circulation: Physiological and Clinical Implications (2017) [PDF]
Anna L. Goldman, Shalender Bhasin, Frederick C.W. Wu, Meenakshi Krishna, Alvin M. Matsumoto, and Ravi Jasuja
Calculated free testosterone using an algorithm that incorporates experimentally observed nonlinear binding dynamics and allosteric interaction between binding sites
The computational algorithm based on this novel multistep ensemble allosteric model (EAM) (34) of testosterone binding to SHBG provided estimates of free testosterone levels that closely matched free testosterone levels measured using the equilibrium dialysis method in samples derived from men and women in two randomized clinical trials (220, 221). The calculated free testosterone level obtained using the prevailing linear model was systematically lower than those measured by equilibrium dialysis. In Table 4, we show that calculated free testosterone values across age deciles in the Framingham Heart Study computed by the linear model are lower than those computed by the allosteric model. The EAM model is based on experimentally derived binding affinity and dynamics, which can be verified experimentally and improved upon with additional information about other variables that determine free testosterone concentrations.
Clinical Implications and Recommendations
Male hypogonadism is a clinical condition characterized by the presence of typical signs and symptoms in the setting of consistently low serum testosterone concentrations. The Endocrine Society guidelines currently suggest measuring free testosterone levels in men in whom total testosterone concentrations are near the lower limit of the normal range and in men with conditions that affect SHBG concentrations and render total testosterone a less reliable index of gonadal function (206). If the free hormone hypothesis is correct, free testosterone should serve as the benchmark for biochemical confirmation of hypogonadism. Accurate determination of free testosterone values is therefore central to an accurate diagnosis of hypogonadism.
The direct analog assays for free testosterone determination are inaccurate and should not be used. However, a confluence of factors related to the regulatory process, economic considerations, and difficulties in performing equilibrium dialysis methods in many hospital laboratories has led to their surprising endurance despite their known inaccuracy. Historically, laboratory-certifying bodies, such as the Clinical Laboratory Improvement Amendments, have certified laboratories and assays mostly on the basis of process measures; unlike the CDC and its Hormone Assay Standardization program for testosterone, these bodies have generally not required accuracy-based benchmarks. Similarly, the requirement in the assay approval process for demonstration of comparability to a previously approved assay enables new tracer analog assays to be approved because they can demonstrate comparability to previously approved analog methods.
Equilibrium dialysis is the reference method for free testosterone determination, but this assay is not always available to clinicians in all hospital laboratories; in addition, there are substantial interlaboratory variations because of the lack of standardization of assay conditions, making it difficult for practicing endocrinologists to interpret free testosterone levels. Mechanisms to harmonize the equilibrium dialysis procedure across laboratories are needed. Until equilibrium dialysis methods can be standardized across laboratories, a computational framework that accurately captures the dynamics of testosterone to SHBG and HSA interactions in calculating free testosterone values is an unmet need for precise clinical diagnosis. The EAM appears to be an accurate and testable model for calculating free testosterone levels, but this model needs further validation in large populations.
* The EAM appears to be an accurate and testable model for calculating free testosterone levels, but this model needs further validation in large populations.
The new dynamic model leads to the reconsideration of several dogmas related to testosterone's binding to SHBG and has important physiologic and clinical implications.
*First, the fraction of circulating testosterone that is free is substantially greater (2.9±0.4%) than has been generally assumed (% cFTV 1.5±0.4%).
*Second, percent FT is not significantly related to total testosterone over a wide range of total testosterone concentrations. However, the percent FT declines as SHBG concentrations increase, although it does not decline as precipitously as predicted by Vermeulen's model. Due to the allostery between the two binding sites, SHBG is able to regulate FT levels in a much larger dynamic range.
Key points:
EAM (cFTZ) SHBG: T binding
*Intra-dimer complex allostery suggests that SHBG can regulate FT fraction over a wide range of total testosterone concentrations without getting saturated.
*Indeed, it was found that percent FT calculated using the new model changed very modestly over a wide range of total testosterone concentrations.
*Due to the allostery between the two binding sites, SHBG is able to regulate FT levels in a much larger dynamic range.
Even then it still needs further validation which is going to happen during Phase II.
There has been an ongoing effort behind the scenes to provide further proof of the validity of the TruT™algorithm (cFTZ).
You and I let alone everyone in the know including top researchers in the field/medical community is waiting on the results/data from Phase II.
You have no idea how much has been invested in this project.
10 years in the making and I would say they are sitting on a shitload of data.
As I have stated numerous times on the forum!
Patiently waiting on the completion of Phase II for the TruT™algorithm (cFTZ) let alone standardization and harmonized reference ranges for Free testosterone which is in the works as we speak.
Ravi let alone Bhasin is confident about the validity/soon-to-be commercialization of the TruT™algorithm (cFTZ).
It's going to happen.
*The phase II program will provide validation of the TruTTM algorithm in the two most common clinical indications for free T measurement? men suspected of hypogonadism and altered SHBG levels, and women with hyperandrogenic disorders

www.sbir.gov
Jasuja, Ravi
The measurement of testosterone (T) levels is central to the diagnosis of androgen disorders, such as hypogonadism in men and polycystic ovary syndrome (PCOS) in women. Circulating T is bound with high affinity to sex hormone-binding globulin (SHBG) and with substantially lower affinity to albumin; only the free fraction is biologically active. Conditions that affect SHBG concentrations, such as aging and obesity, alter total but not free T concentrations; in these conditions, the determination of free T is necessary to obtain an accurate assessment of androgen status. The tracer analog method, the most widely used method for free T, has been shown to be inaccurate. The equilibrium dialysis method, considered the reference method, is technically difficult to implement and standardize, and is not available in most hospital laboratories, leading the Endocrine Society's Expert Panel to conclude that ?? the calculation of free testosterone is the most useful estimate of free testosterone in plasma?? Therefore, there is an unmet need for algorithms that provide accurate estimates of free T that match those derived from equilibrium dialysis. We have designed a novel and accurate TruTTM algorithm for the determination of free T, based on the characterization of testosterone's binding to SHBG using modern biophysical techniques. We have discovered that testosterone's binding to SHBG is a dynamic multistep process that includes allosteric interaction between the two binding sites on an SHBG dimer. Our computational framework incorporates the correct binding parameters derived experimentally in these studies, the non-linear dynamics in T: SHBG association, and allostery
In phase I studies, we demonstrated that the TruTTM algorithm provides accurate free T values that match those obtained using the equilibrium dialysis in healthy and hypogonadal men. We have also shown that the binding parameters that have formed the basis of previous equations (e.g., Vermeulen) are incorrect, and that free T values derived using these equations deviate substantially from free T measured by equilibrium dialysis. The phase I studies have led to the adoption of the TruTTM algorithm at several institutions.
The phase II program will continue the development of the TruTTM algorithm by validating it in common conditions characterized by altered SHBG concentrations, such as obesity and aging (AIM 1), in healthy women across the menstrual cycle, and in women with PCOS (Aim 2). We will generate population-based reference ranges for free T (Aim 3). Phase II also includes plans for the commercialization of the TruTTM algorithm using a HIPAA-compliant infrastructure for its clinical adoption
The phase II program will provide validation of the TruTTM algorithm in the two most common clinical indications for free T measurement? men suspected of hypogonadism and altered SHBG levels, and women with hyperandrogenic disorders. It will also enable the development of a HIPAA-compliant platform that can be embedded into the electronic medical record for wider clinical adoption and for improving clinical care
Phase II: Research and Commercialization of TruT Algorithm (Sep.15, 2014-May 31, 2022)
View attachment 23703
Reassessing Free-Testosterone Calculation by Liquid Chromatography-Tandem Mass Spectrometry Direct Equilibrium Dialysis (2018) [PDF]
Tom Fiers, Frederick Wu, Paolo Moghetti, Dirk Vanderschueren, Bruno Lapauw, and Jean-Marc Kaufman
Assessment of FT might improve precision in the diagnosis of hyperandrogenism in women and hypogonadism in men, in particular when total T levels are borderline and in situations known to alter SHBG levels (9, 10). Equilibrium dialysis (ED)– or ultrafiltration (UF)-based methods, considered the reference for determination of FT, were, in the past, mostly indirect, with the addition of a labeled T tracer, determination of the percentage of free labeled T and calculation of FT from the percentage of free labeled T and total T. ED and UF methods are technically challenging and have potential pitfalls; reliable implementation is labor intensive and poorly suited for high throughput (4, 8)
Therefore, there has been widespread use of easier-to-implement surrogate estimates of FT. The direct analog tracer-based immunoassays do not reliably reflect true FT and should not be used (9). Most frequently used in clinical and research settings are calculated estimates of serum FT levels based on serum total T and SHBG levels with or without the actual serum albumin concentrations (11). The simple FT index of total T over SHBG is less reliable and now generally abandoned in favor of alternative calculations (9, 12). Equations derived from the general law of mass action, with association constants for T binding to SHBG and albumin values derived from in vitro experiments (8, 13, 14), are frequently used in clinical practice. The version proposed by Vermeulen et al. (8) has been the most widely applied. Equations empirically developed by regression modeling on large sets of values for FT as determined with a reference method have also been used (11, 15). Although calculations seem to have performed well in many studies, acknowledging that they all have inherent limitations, there is ongoing controversy about the accuracy of calculated estimates of FT. It has been suggested that equations derived from the law of mass action are based on an inaccurate model of T binding to SHBG and/or that the chosen set of binding constants is not appropriate (4, 16). In this context, the alternative dynamic allosteric model of T binding to SHBG recently put forward (4, 17) may have far-reaching implications. If confirmed, this new model not only invalidates most of the methods commonly used for calculating FT levels but also suggests that the percentage FT data obtained by most established methods including ED- or UF-based assays are incorrect.
All this translates into uncertainty as how to best calculate FT and its true measured value. In the current study, we used a state-of-the-art direct ED method to reassess FT in sets of representative serum samples. This method takes advantage of the ability of a highly sensitive and accurate measurement of T by liquid chromatography-tandem mass spectrometry (LC-MS/MS) to reliably measure the low FT concentration directly in the dialysate after ED. This more straightforward method avoids potential sources of inaccuracy in indirect ED, such as those resulting from tracer impurities or from measures to limit their impact (e.g., sample dilution). We then used the measured FT results to re-evaluate some characteristics of two more established and more recently proposed calculations for the estimation of FT.
Calculated estimations of FT
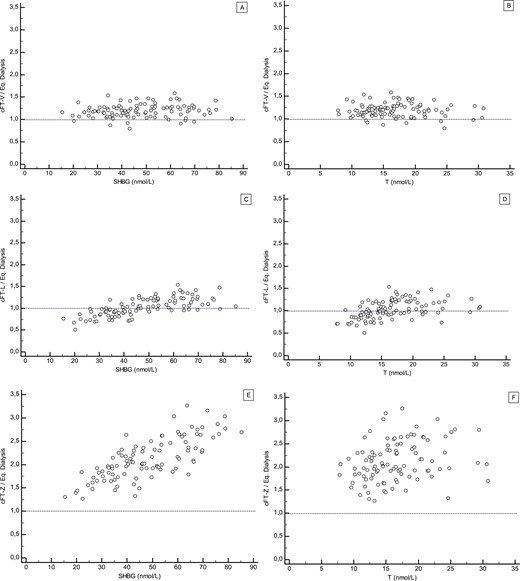
FT level was calculated from total T, SHBG, and albumin serum levels according to the three following methods: (1) an equation based on the law of mass action as published by Vermeulen et al. (8) (cFT-V); (2) two empirically derived formulae (for men, the formula for T . 5 nM was used; for women, the formula,5 nM was used) as published by Ly and Handelsman (15) (cFT-L); and (3) according to a calculation based on a multistep, dynamic, allosteric model of testosterone binding to SHBG as published by Zakharov et al. (17) (cFT-Z). The values for cFT-Z from the EMAS samples (calculated with original T and SHBG from EMAS) were provided by Dr. R. Jasuja, Boston, MA, to the EMAS investigators. We had no direct access to the algorithm for cFT-Z; therefore, we were unable to present any data on cFT-Z for the samples from SIBLOS and from women.
Discussion
In this study, we reassessed FT with a state-of-the-art direct ED assay. The findings support and further validate the basic tenets of FT in men and women as previously established with traditional indirect ED and UF methodologies. They further highlight important differences in commonly used or recently proposed algorithms for deriving calculated FT values from serum total T and SHBG (and albumin) levels compared with FT measurement by direct ED.
Calculated estimates of FT
Calculated FT estimates are critically dependent on the reliability and calibration of the T and SHBG assays (9, 34, 35). Furthermore, they are based on the assumption of a normal steady-state protein-binding characteristic for T, which is not the case in every individual. Any equation will incorrectly estimate FT in situations such as the presence of large concentrations of competing steroids, large deviations from physiological protein concentrations, or rare genetic variants of SHBG affecting T binding affinity (3, 8). Besides these occasional problems, more systematic differences between FT estimates depending on the used equation and as compared with measured FT have been reported (11, 12, 28).
Our results show that cFT-V is strongly correlated to FT measured by direct ED but systematically overestimates FT by 20% to 30%. This confirms our prior findings (22, 23) and those of others (28). The relation between cFT-V and measured FT is linear and independent of serum T, SHBG, and albumin levels. This is a strength of the cFT-V approach for clinical use because assessment of FT is most relevant in patients with high or low SHBG levels. This also indicates that the equation derived from the mass action law predicts the binding behavior of T to serum proteins quite well. The systematic positive bias observed for cFT-V has to be taken into account when comparing FT levels across different methods. This bias likely reflects that the in vitro determined association constants used in the equation are imperfect approximations of the actual in vivo association constants for binding of T to SHBG and albumin. FT measured with our prior in-house indirect ED, which involves a correction for serum dilution effect with the use of the same basic equation and set of association constants as in cFT-V (1, 8), shows a similar positive bias compared with FT measured by direct ED (data not shown). This explains our prior findings of correlation without a bias between cFT-V and FT by indirect ED (8, 35).
Our results for cFT-L show that median cFT-L approximates closely median FT by direct ED in men and women, as calculated with the equations intended for high and low T levels, respectively (16). However, an agreement between cFT-L and measured FT was found to be strongly dependent on SHBG and T levels. Thus, cFT-L performs differently depending on serum T and SHBG levels and increasingly underestimates FT at low SHBG or low T levels. This may limit the accuracy of cFT-L in hypogonadal men with low T levels and in obese men or women with PCOS with low SHBG levels.
The cFT-Z values reported here have been supplied by the authors who reported data for cFT-Z in the EMAS cohort in the publication describing their multistep, dynamic, allosteric model to calculate FT (17). We requested access to the cFT-Z algorithm from the research group that developed this allosteric model algorithm. However, at the time of completion of this work, we had not been able to gain direct access to the algorithm. Therefore, it was not possible to make comparisons with cFT-Z for all three cohorts. This is a limitation of the current study that is beyond our control. We felt it important to evaluate cFT-Z in the current study because the results obtained by the authors according to their allosteric model to replicate the dimeric binding of T to SHBG differed substantially from the model based on the law of mass action (4, 17). Using the allosteric model, they reported higher FT% in men of 3% to 5% and that cFT-V substantially underestimated FT compared with their findings for FT by dialysis (17). Our results for the EMAS samples, indeed, do reproduce their finding that cFT-Z values are markedly higher than cFT-V values. Similarly, cFT-Z values are much higher compared with cFT-L. However, in contrast to their findings, our results also show that cFT-Z is markedly higher (about double) compared with FT measured by direct ED. Moreover, the accuracy of cFT-Z as reflected in the ratio of cFT-Z over measured FT was strongly dependent on serum SHBG levels and, to a lesser degree, on T and albumin levels.
* At present, it is unclear what underlies the apparent discrepancy between the results reported by Zakharov et al. (17) and the findings in the current study performed on the same set of samples. A factor involved may be differences in ED methods between laboratories giving discrepant measured FT results. The descriptive nature of this study does not allow us to address possible merits or demerits of basic assumptions on which the allosteric model is based.
In summary, for none of the three evaluated equations does calculated FT perfectly match FT measured with a state-of-the-art direct ED assay. However, there are distinct differences in how the respective equations behave. cFT-Z appears far off target relative to the results of direct ED in this study as well as compared with a substantial body of published data obtained with a variety of ED- or UF-based methods. Although cFT-L performs well in the midrange levels of serum T and SHBG, the dependence of its accuracy on T and SHBG levels has clinical implications (e.g., underestimation by cFT-L of FT at low SHBG concentrations could impair the ability to detect hyperandrogenism in PCOS or lead to overdiagnosis of hypogonadism in obese men). Although a systematic positive bias affects the external comparability of cFT-V with other methods, the consistency of its performance compared with directly measured FT, independent of serum T and SHBG levels, ensures strong internal validity. This is an important asset for clinical applications of FT assessments in patients with widely different T and SHBG levels. The cFT-V equation admittedly is a simplified representation of the binding of T to its binding proteins. Moreover, there is room for refinement of the association constants implemented in the equation. Nevertheless, contrary to what has been suggested (4, 17, 28, 36), our results do confirm that cFT-V is based on a valid model of T binding to SHBG.
In conclusion, calculated estimates of FT have inherent limitations with distinct and clinically important differences in the performance of different algorithms. Of the three methods, we evaluated in this study, cFT-V, albeit systematically overestimating FT, most robustly approximated directly measured FT in samples representative of a broad range of T and SHBG levels. There is a need for collaborative efforts to further validate and harmonize methods to measure and calculate FT levels.
Points to keep in mind:
*Although a systematic positive bias affects the external comparability of cFT-V with other methods, the consistency of its performance compared with directly measured FT, independent of serum T and SHBG levels, ensures strong internal validity. This is an important asset for clinical applications of FT assessments in patients with widely different T and SHBG levels. The cFT-V equation admittedly is a simplified representation of the binding of T to its binding proteins. Moreover, there is room for refinement of the association constants implemented in the equation. Nevertheless, contrary to what has been suggested (4, 17, 28, 36), our results do confirm that cFT-V is based on a valid model of T binding to SHBG
* Although calculations seem to have performed well in many studies, acknowledging that they all have inherent limitations, there is ongoing controversy about the accuracy of calculated estimates of FT. It has been suggested that equations derived from the law of mass action are based on an inaccurate model of T binding to SHBG and/or that the chosen set of binding constants is not appropriate (4, 16). In this context, the alternative dynamic allosteric model of T binding to SHBG recently put forward (4, 17) may have far-reaching implications. If confirmed, this new model not only invalidates most of the methods commonly used for calculating FT levels, but also suggests that the percentage FT data obtained by most established methods including ED- or UF-based assays are incorrect
Everyone seems to be forgetting about the Keevil paper that came out the following year!
Assessment of free testosterone concentration (2019) [PDF]
Brian G Keevil, Jo Adaway
Highlights
*Free testosterone may complement the measurement of total serum T, but this view remains controversial and is not universally accepted
*Equilibrium dialysis methods are too complex for routine clinical use
*Equations for calculating free testosterone are inaccurate because they were founded on faulty models of T binding to SHBG
*More accurate equations are needed to calculate free testosterone, based on more detailed knowledge of the binding of testosterone to SHBG.
*Harmonization of T and SHBG assays between laboratories needs to be improved
*The algorithms derived for calculating free T are inaccurate because they were founded on faulty models of testosterone binding to SHBG
*the effects of differences in binding protein constants
The calculation proposed by Vermeulen et al has been the most widely used but the main criticism of all these equations is that the model of binding of T to SHBG may not be accurate, and in addition, the set of binding constants used may not be appropriate (14, 32). SHBG is a homodimeric glycoprotein with a molecular weight of approximately 90 kDa (33) and the distribution of testosterone bound to SHBG is different in males and females. When Estradiol is present, approximately 20% of SHBG binding sites are occupied by testosterone (34). It was previously thought that the two binding sites on the SHBG molecule are equivalent, but using modern biophysical techniques it is now known that the binding sites are not equivalent, and they each bind SHBG with a different affinity (22). As a result of this, alternative models of binding T to SHBG have been advocated (14,22).
Calculated FT (cFT) estimates are based on the assumption that there is normal steady-state protein binding for T and the equations are dependent on the reliability and accuracy of both the T and SHBG assays (6, 35, 36). All of the equations will estimate free T incorrectly when the protein concentrations differ widely from physiological values, if there are large concentrations of competing steroids, or if the SHBG binding affinity is affected by a rare genetic variant (12, 37). Depending on the equation used, systematic differences between free T estimates have been reported compared with measured free T (18, 21, 30). Discrepancies between free T measured using equilibrium dialysis and cFT are most likely caused by erroneous modeling of testosterone binding to SHBG.
Recent work shows that cFT-Vermeulen is strongly correlated to free T measured by the reference method (direct equilibrium dialysis), but free T is overestimated by 20 to 30%, thus agreeing with previous work (21, 38, 39). However, the relationship between cFT-Vermeulen and measured free T was found to be linear and independent of serum T, albumin, and SHBG concentrations. The lack of reliance on SHBG in the Vermeulen equation was thought to be a strength of the cFT-Vermeulen since the assessment of free T is especially important in patients at the extremes of the SHBG concentration range. The bias is probably due to imperfect estimations of the association constants for the binding of T to SHBG and albumin, as discussed above, and this would need to be allowed for when comparing different methods for cFT.
Equations for calculating FT are inaccurate because they were founded on faulty models of T binding to SHBG. Calculated FT methods offer are simple and inexpensive and may offer the best way forward, but more accurate equations are needed and these must be based on more detailed knowledge of the complicated binding of testosterone to SHBG.
Take home points:
*Depending on the equation used, systematic differences between free T estimates have been reported compared with measured free T (18, 21, 30). Discrepancies between free T measured using equilibrium dialysis and cFT are most likely caused by erroneous modeling of testosterone binding to SHBG
*Recent work shows that cFT-Vermeulen is strongly correlated to free T measured by the reference method (direct equilibrium dialysis), but free T is overestimated by 20 to 30%, thus agreeing with previous work (21, 38, 39)
*However, the relationship between cFT-Vermeulen and measured free T was found to be linear and independent of serum T, albumin, and SHBG concentrations
*The lack of reliance on SHBG in the Vermeulen equation was thought to be a strength of the cFT-Vermeulen since the assessment of free T is especially important in patients at the extremes of the SHBG concentration range
*The bias is probably due to imperfect estimations of the association constants for the binding of T to SHBG and albumin, as discussed above, and this would need to be allowed for when comparing different methods for cFT.
Everyone still seems to be caught up on the Fiers paper which dropped in 2018 yet the data/results have not even come out for Phase II: Research and Commercialization of TruT Algorithm for Free Testosterone.
Much going on behind the scenes and more to come.
He is already pushing the use of the newer calculated method!
Look over his most recent paper:
Optimizing Diagnostic Accuracy and Treatment Decisions in Men With Testosterone Deficiency (2021) [PDF]
Shalender Bhasin, MB, BS *, Noelle Ozimek, MSc
Optimizing Diagnostic Accuracy and Treatment Decisions in Men With Testosterone Deficiency (2021) Shalender Bhasin, MB, BS *, Noelle Ozimek, MSc Abstract Objective: This narrative review offers a guideline-based approach for optimizing diagnostic evaluation and treatment decision-making in...

www.excelmale.com
*equations that are based on a linear model of testosterone’s binding to SHBG assume a fixed binding affinity (approximately 1 nM)31 and ignore the competing presence of other sex steroids, such as dihydrotestosterone and estradiol
*Recent studies using modern biophysical techniques have suggested that the binding of testosterone and estradiol to an SHBG dimer is a dynamic process that involves allosteric interactions between binding sites on each of the 2 SHBG monomers such that the binding affinities of the 2 sites are not equivalent.36,39 The binding of a ligand to the first monomer influences the conformational and energetic states of both the monomers.39 The estimation of free testosterone concentration based on an ensemble allosteric model provides a close approximation of concentrations measured using equilibrium dialysis36;
*the computations of free testosterone concentrations using the ensemble allostery model can be obtained at TruT Free Testosterone Calculator by FPT
*Because of dynamic changes in the binding affinity of SHBG upon ligand binding, depending on the ligand and SHBG concentrations, no equation can accurately estimate free testosterone concentration under all conditions.39
*A reference range for free testosterone, using an ensemble allostery method that was validated against the equilibrium dialysis method using data from the Framingham Heart Study and the European Male Aging Study, has been published.36
Again it's been 4 years since Fiers's paper dropped and Bhasin is still taking a firm stance on backing TruT™algorithm (cFTZ).
Listen to his more recent Endocrine Grand Rounds presentation (March 2022) he is still standing his ground when it comes to the linear law-of-mass action equation (cFTV).
*the Vermeulen equation and others that assume a fixed Kd are just conceptually wrong and our data show it clearly that this model is completely wrong
*so the Vermeulen model or most of the linear equations underestimate free testosterone concentrations and the ensemble allosteric model (EAM) based upon our experimental data matches total testosterone within the range in which we have validated this
Bold statement I would say!
Put money on it that Bhasin and his team are sitting on something big and they are going to drop the ball (results/data) from Phase II: Research and Commercialization of TruT Algorithm for Free Testosterone once standardization and harmonized reference ranges for Free testosterone come to fruition.
This is far from over and definitely not a one-and-done!
post #5/6

www.excelmale.com
24:05-37:00 (Endocrine Grand Rounds presentation March 2, 2022)
28:36-31:58 (cFTV/cFTZ)
Shalender Bhasin :
*the calculated free testosterone is based on the simplistic notion that total testosterone is linearly related to free testosterone concentration and so you can compute total testosterone if you know the binding affinity and the concentrations of SHBG and albumin discounting orosomucoid and cortisol binding globulin and many people just ignore albumin because of the perception that albumin-bound testosterone remains relatively in constant
*and there are some empirically derived equations
*and I'll show you that the linear equations such as the Vermeulens equation that is based on the simplistic idea that one molecule of testosterone binds to one molecule of SHBG at a single binding site with a fixed binding affinity of 1 nanomolar (nM) to form a testosterone SHBG complex
*what are studies have shown is that testosterone binding to SHBG and we have shown similar data with estradiol which I'll show you in a minute
*and that this binding is a multi-step dynamic process
*so SHBG circulates as a dimer in circulation and this dimer is very tightly bound and it takes 8 nanomolar (nM) to dissociate the dimer but upon binding of the first testosterone to the first binding pocket in the first monomer there's a change in conformation of the first monomer as well as change in the conformation of the second monomer due to the allosteric interaction between the two binding pockets such that the binding of testosterone to the second binding pocket in the second monomer occurs with a different binding affinity and this process is very dynamic so the Kd is not fixed therefore the linear equations such as the Vermeulen equation and others that assume a fixed Kd are just conceptually wrong and our data show it clearly that this model is completely wrong
*so the Vermeulen model or most of the linear equations underestimate free testosterone concentrations and the ensemble allosteric model (EAM) based upon our experimental data matches total testosterone within the range in which we have validated this
*so let me show you some additional data which persuade me that no equation can ever be an accurate measure of the free testosterone at all levels of SHBG, testosterone, estradiol, DHT, and albumin under all conditions in men in women