madman
Super Moderator
Context: Assessment of free testosterone (FT) might help evaluate androgen status in patients with borderline total testosterone (T) and/or altered sex hormone–binding globulin (SHBG) levels. However, the validity of different methods to measure FT is debatable.
Methods: Serum from 183 women and 146 men was analyzed using equilibrium dialysis (ED), with FT directly measured by liquid chromatography–tandem mass spectrometry. FT calculation was reevaluated for the mass action law–based equation according to Vermeulen (cFT-V), empirical equations according to Ly (cFT-L), and a proposed calculation based on a multistep, dynamic,allosteric model according to Zakharov (cFT-Z).
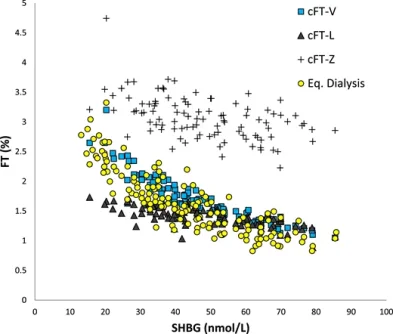
Results: FT level analyzed by ED [median,13 pmol/L (1.2% of T) in women; 248 pmol/L (1.5% of T) in men] was strongly inversely correlated to SHBG level, significantly to albumin level in women, and only weakly to SHBG level in men. The median [percentile (p) range, 2.5 to 97.5] ratios of calculated FT (cFT) over ED-FT (from European Male Aging Study samples) were 1.19 (0.9 to 1.47), 1.00 (0.69 to 1.42), and 2.05 (1.26 to 3.26) for cFT-V, cFT-L, and cFT-Z, respectively. The ratio for cFT-V was not significantly affected by SHBG, T, or albumin levels (p range, 0.17 to -0.01); ratios for cFT-L and cFT-Z were affected (P < 0.05 and P < 0.001, respectively) and strongly correlated with SHBG levels (p = 0.72 and 0.75, respectively). Rank correlations between cFT% and ED-FT% (for men) were 0.62, 0.74, and 0.89 for cFT-Z, cFT-L, and cFT-V, respectively.
Conclusion: FT results by direct ED confirm prior FT data from indirect ED and ultrafiltration methodologies. Calculations have inherent limitations, with clinically important differences among evaluated equations: cFT-V, although overestimating FT level, appears the most robust approximation, largely independent of SHBG, albumin, and T levels. (J Clin Endocrinol Metab103: 2167–2174, 2018)
Methods: Serum from 183 women and 146 men was analyzed using equilibrium dialysis (ED), with FT directly measured by liquid chromatography–tandem mass spectrometry. FT calculation was reevaluated for the mass action law–based equation according to Vermeulen (cFT-V), empirical equations according to Ly (cFT-L), and a proposed calculation based on a multistep, dynamic,allosteric model according to Zakharov (cFT-Z).
Results: FT level analyzed by ED [median,13 pmol/L (1.2% of T) in women; 248 pmol/L (1.5% of T) in men] was strongly inversely correlated to SHBG level, significantly to albumin level in women, and only weakly to SHBG level in men. The median [percentile (p) range, 2.5 to 97.5] ratios of calculated FT (cFT) over ED-FT (from European Male Aging Study samples) were 1.19 (0.9 to 1.47), 1.00 (0.69 to 1.42), and 2.05 (1.26 to 3.26) for cFT-V, cFT-L, and cFT-Z, respectively. The ratio for cFT-V was not significantly affected by SHBG, T, or albumin levels (p range, 0.17 to -0.01); ratios for cFT-L and cFT-Z were affected (P < 0.05 and P < 0.001, respectively) and strongly correlated with SHBG levels (p = 0.72 and 0.75, respectively). Rank correlations between cFT% and ED-FT% (for men) were 0.62, 0.74, and 0.89 for cFT-Z, cFT-L, and cFT-V, respectively.
Conclusion: FT results by direct ED confirm prior FT data from indirect ED and ultrafiltration methodologies. Calculations have inherent limitations, with clinically important differences among evaluated equations: cFT-V, although overestimating FT level, appears the most robust approximation, largely independent of SHBG, albumin, and T levels. (J Clin Endocrinol Metab103: 2167–2174, 2018)
Attachments
-
[email protected]319.1 KB · Views: 294